导数和微分

1 拉格朗日中值定理

如果\(f(x)\)满足以下条件：

• 在闭区间\([a,b]\)上连续
• 在开区间\((a,b)\)内可导

那么有如下结论：

在\((a,b)\)上存在一点\(\xi\)，使得

\[ f'(\xi)=\dfrac{f(b)-f(a)}{b-a} \]

2 Taylor Formula

\[ f(x)=f(x-x_0)+f'(x_0)(x-x_0)+o(x) \]

\[ f(x)=f(x-x_0)+\sum_{i=1}^{\infty}f^{(i)}(x_0)\dfrac{(x-x_0)^n}{i!} \]

常用泰勒展开式

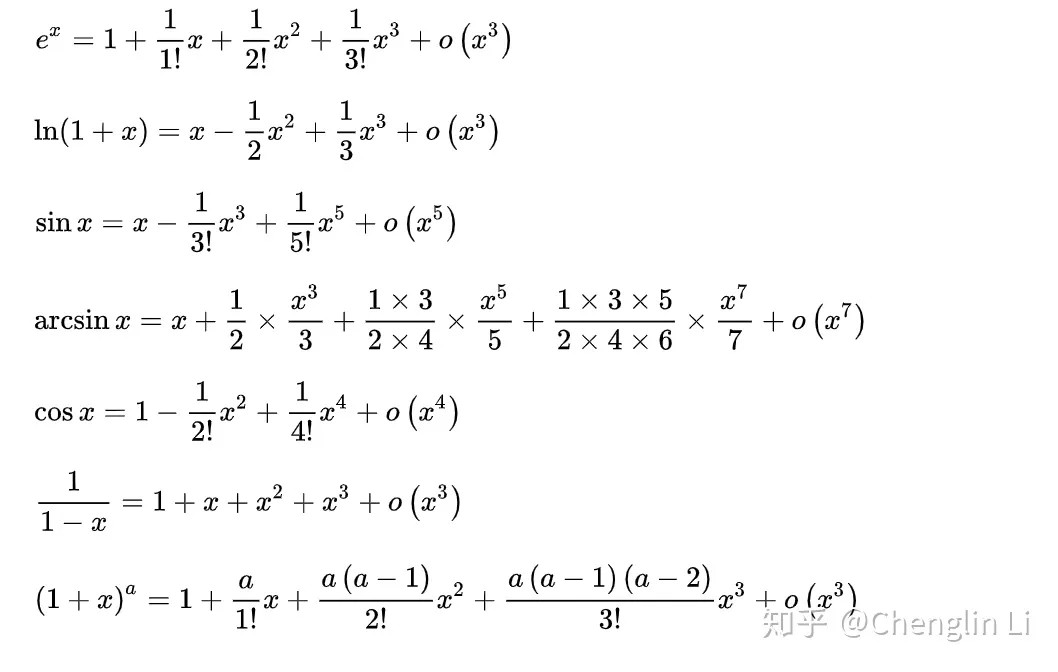
3 有理化

求极限时，若分子或分母上出现了根式做差，很多时候可以利用平方差公式进行分子或分母有理化，或三次方公式也可以。

4 导数定义

给定函数\(f(x)\)，若极限

\[ \lim_{\Delta x\to0}\dfrac{f(x_0\pm\Delta x)-f(x_0)}{\Delta x} \]

存在，且相等则称其为\(f(x)\)在\(x_0\)处的导数，并称\(f(x)\)在\(x=x_0\)处可导。

5 导数的存在性和极限

1. \(f(x)\)在\(x_0\)处可导，则\(f(x)\)在\(x_0\)处连续。但\(\lim_{x\to x_0}f'(x)\)存在，不能导出则\(f(x)\)在\(x_0\)处连续
2. 如果\(f(x_0)\)在\(x_0\)附近的某空心邻域内可导且\(f'(x)\)在\(x_0\)处的极限为\(A\)，那么
   1. 如果\(f'(x)\)在\(x_0\)处的极限为\(A\)，\(f(x)\)在\(x_0\)处不连续，那么\(f'(x_0)\)不存在
   2. 如果\(f'(x)\)在\(x_0\)处的极限为\(A\)，\(f(x)\)在\(x_0\)处连续，那么\(f'(x_0)=A\)
   3. \(f'(x)\)在\(x_0\)处的极限等于无穷，那么\(f'(x_0)\)不存在
   4. 如果\(f'(x)\)在\(x_0\)处的极限不等于无穷，也不存在，此时不能确定\(f'(x_0)\)的存在性

6 高阶无穷小量

若\(f,g\)在\(x_0\)处的极限都是0，并且有

\[ \lim_{x\to x_0}\dfrac{f(x)}{g(x)}=0 \]

则称\(f\)为\(g\)在\(x=x_0\)处的高阶无穷小量，记做

\[ f(x)=o(g(x)) \]

7 一阶微分的形式不变性和高阶微分没有此性质

已知\(y=f(u),u=\varphi(x)\)，那么进行变量替换时有

\[ \mathrm dy=f'(u)\mathrm du=f'(u)\varphi'(x)\mathrm dx \]

这称为一阶微分的形式不变性，而二阶微分不具有这个性质，而是

\[ \begin{aligned} \mathrm d^2y &=f'(u)\mathrm d^2u+f''(u)\mathrm du^2\\ &=\left[ f'(u)\varphi''(x)+f''(u)(\varphi'(x))^2\right] \mathrm dx^2 \end{aligned} \]

上式是通过将\(u\)看作以\(x\)为自变量的函数，而不是自变量，对一阶微分进行第二次微分得出的，进行第二次微分时，多出了一项，而且求微分的次数越高，多出的项越多。

如果\(u\)是自变量，那么依旧有

\[ \mathrm d^2y=f''(u)\mathrm du^2 \]

求微分时变量替换的问题

所以在求微分时，只能一次一次求，不能一步到位。

或者说，求导数运算被认为是两个微分符号相除，而是一整个微分算子\(\dfrac{\mathrm d}{\mathrm dx}\)作用在函数上。

例如求\(\dfrac{\mathrm d^2y}{\mathrm dx^2}\)不能直接求\(\dfrac{\mathrm d^2y}{\mathrm du^2}\cdot\left(\dfrac{\mathrm du}{\mathrm dx}\right)^2\)

因为它实际上是

\[ \dfrac{\mathrm d^2y}{\mathrm dx^2}=f''(u)\left(\dfrac{\mathrm du}{\mathrm dx}\right)^2+f'(x)\dfrac{\mathrm d^2u}{\mathrm dx^2} \]

8 渐近线

如果关于函数\(f(x)\)的极限

\[ \lim_{x\to+\infty}\dfrac{f(x)}{x} \]

存在，那么这个函数有一个向\(x\)轴正方向的渐近线，其斜率\(k\)等于上述极限，截距

\[ b=\lim_{x\to+\infty}(f(x)-kx) \]

注释

如果\(f(x)\)同时在\((c,+\infty)\)上可导，那么由L’Hopital’s Rule可以立即得到

\[ k=\lim_{x\to+\infty}f'(x) \]

上述讨论在\(x\to-\infty\)时也成立，函数在\(x\)轴负方向也有一条渐近线，如果正负两根渐近线重合，视为一条渐近线。