三角函数

1 三角函数六角图

三角函数六角图

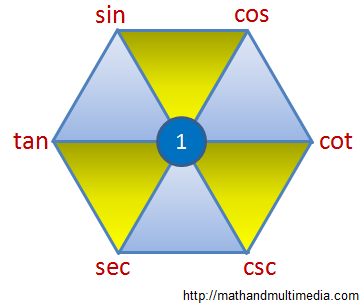
在图中，对角线表示倒数，黄色三角形的邻角表示具有恒等关系，具体如下

• \(\sin^2x+\cos^2=1\)
• \(\sec^2x-\tan^2x=1\)
• \(\csc^2x-\cot^2x=1\)

2 三角函数和差化积公式

\[ \begin{aligned} \sin\alpha+\sin\beta &=2\sin\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2}\\ \sin\alpha-\sin\beta &=2\cos\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2}\\ \cos\alpha+\cos\beta &=2\cos\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2}\\ \cos\alpha-\cos\beta &=-2\sin\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2} \end{aligned} \]

3 三角函数嵌套反三角函数

前提条件\(x\in(0,\dfrac{\pi}{2})\)

\[ \begin{aligned} &\sin\arccos x=\cos\arcsin x=\sqrt{1-x^2}\\ &\sin\arctan x=\dfrac{x}{\sqrt{1+x^2}}\\ &\cos\arctan x=\dfrac{1}{\sqrt{1+x^2}}\\ &\tan\arcsin x=\dfrac{x}{\sqrt{1-x^2}}\\ &\tan\arccos x=\dfrac{\sqrt{1-x^2}}{x} \end{aligned} \]